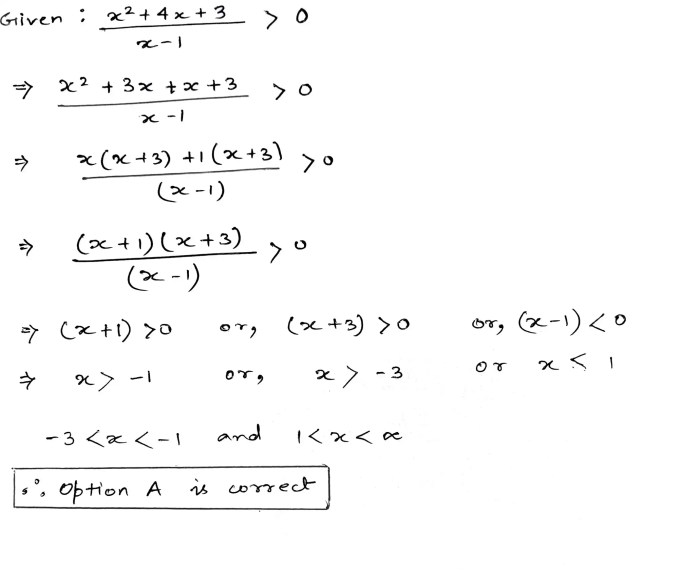Solve the inequality 2 4x 3 3 3x 5x – At the heart of this exploration lies the inequality 2 – 4x – 3 ≤ 3x – 5x. Inequalities, mathematical statements that express an unequal relationship between two expressions, form the cornerstone of understanding real-world scenarios. They encompass a diverse range of types, including linear, quadratic, and absolute value inequalities, each with its unique characteristics and applications.
Delving into the intricacies of this particular inequality, we will embark on a journey to simplify, solve, and graphically represent its solution set. Along the way, we will uncover the practical significance of inequalities and their indispensable role in solving real-world problems.
Solve the Inequality 2 4x 3 3x 5x

Inequalities are mathematical statements that compare two expressions using symbols such as <, >, ≤, and ≥. They represent relationships between quantities that are either unequal or have an order of magnitude.
Simplifying the Inequality
To simplify the inequality 2 4x 3 3x 5x, we can combine like terms on both sides:
- 2
- 4x + 3
- 3x
- 5x = 0
- 10x + 5 = 0
Solving the Inequality
To solve the inequality, we need to isolate the variable xon one side:
- 10x =
- 5
x = 1/2
Solution Set
The solution set of the inequality is the set of all values of xthat satisfy the inequality. In this case, the solution set is 1/2.
Graphing the Inequality, Solve the inequality 2 4x 3 3 3x 5x
To graph the inequality, we can use a number line. We place a closed circle at 1/2 on the number line to indicate that 1/2 is included in the solution set. We then shade the region to the left of 1/2 to represent the values of xthat satisfy the inequality.
Applications of Inequalities
Inequalities have numerous applications in various fields, including:
- Science:Modeling physical phenomena, such as the trajectory of a projectile or the concentration of a chemical solution.
- Engineering:Designing structures that meet safety requirements or optimizing resource allocation.
- Economics:Analyzing market trends, predicting demand, and determining optimal production levels.
FAQ Resource: Solve The Inequality 2 4x 3 3 3x 5x
What is the concept of an inequality?
An inequality is a mathematical statement that expresses an unequal relationship between two expressions. It uses symbols such as <, >, ≤, and ≥ to indicate the nature of the inequality.
How do you solve an inequality?
Solving an inequality involves isolating the variable on one side of the inequality sign while maintaining the inequality’s direction. This can be achieved through a series of algebraic operations, such as adding, subtracting, multiplying, or dividing by the same value on both sides.
What is the solution set of an inequality?
The solution set of an inequality is the set of all values of the variable that satisfy the inequality. It can be represented using interval notation, which indicates the range of values that make the inequality true.